This example is taken from the PROPT manual example 44. The example is simular to the previous example Goddard rocket maximum ascent but with slightly different model parameters.
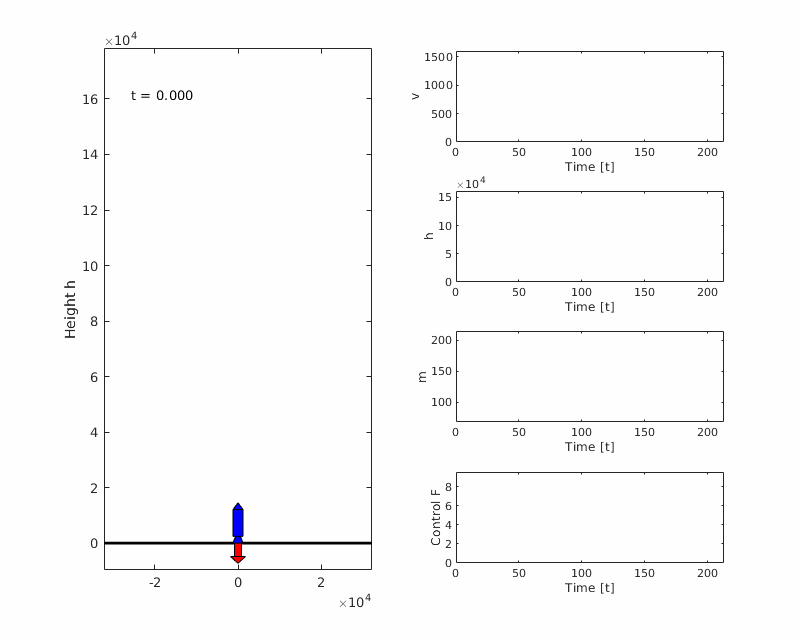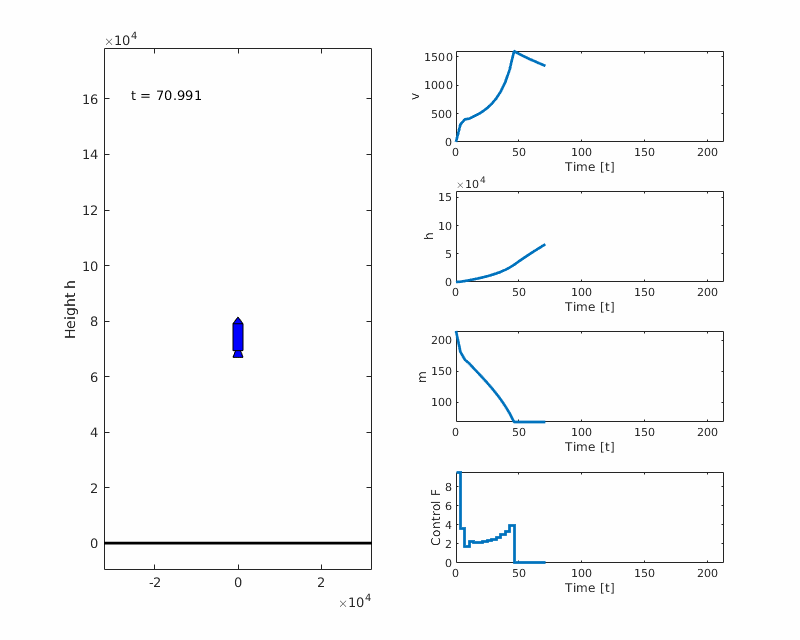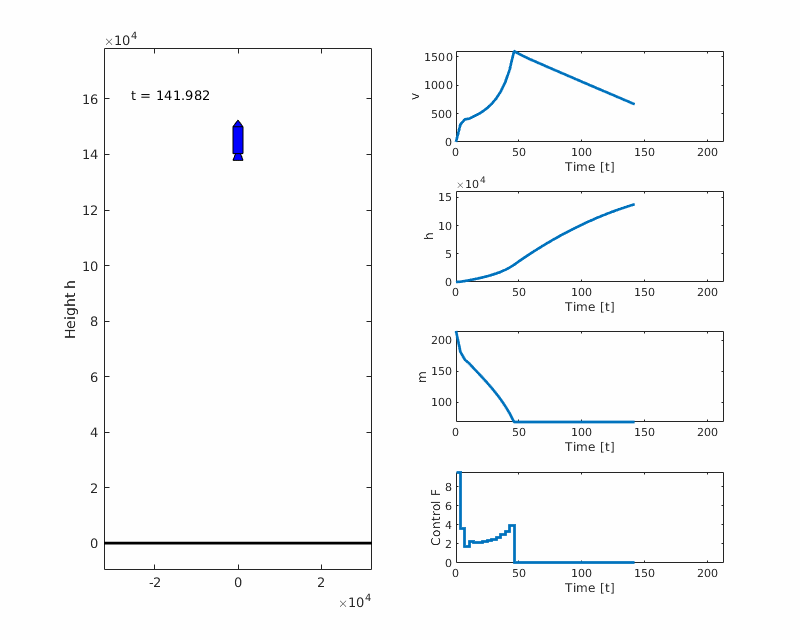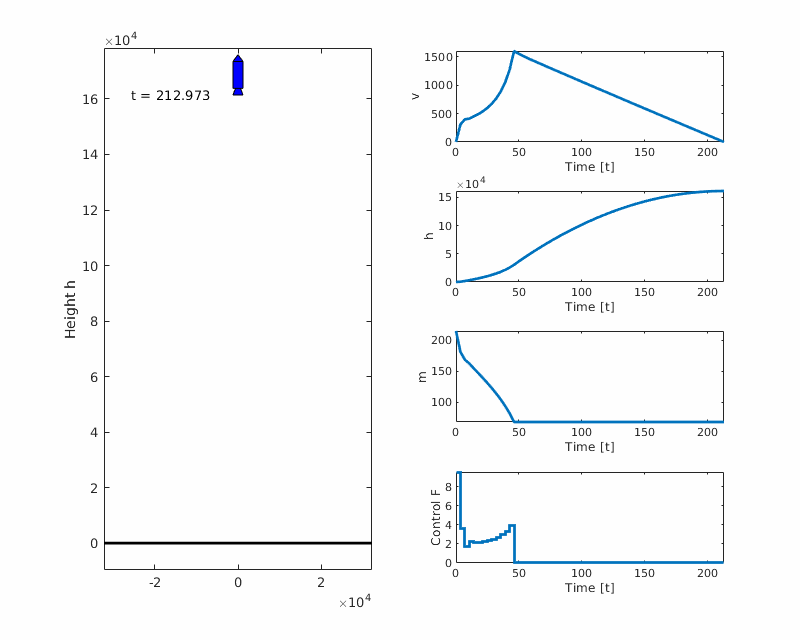
Problem formulation
The problem formulation is the following:
The states are the rocket velocity , the altitude from the ground and mass of the rocket . The rocket burns fuel and expels it out the nozzle creating thrust, in the model the fuel flow rate is the control and the ratio between thrust and change in mass is .
Yop implementation
%% Goddard Rocket, Maximum Ascent
% Author: Dennis Edblom
% Create the Yop system
sys = YopSystem('states', 3, 'controls', 1, ...
'model', @goddardRocketModel);
% Symbolic variables
time = sys.t;
% Rocket signals (symbolic)
rocket = sys.y.rocket;
m0 = 214.839;
mf = 67.9833;
Fm = 9.525515;
% Formulate optimal control problem
ocp = YopOcp();
ocp.max({ t_f( rocket.height ) });
ocp.st(...
'systems', sys, ...
... % initial conditions
{ 0 '==' t_0(time) }, ...
{ 0 '==' t_0(rocket.velocity) }, ...
{ 0 '==' t_0(rocket.height) }, ...
{ m0 '==' t_0(rocket.mass) }, ...
... % Constraints
{ 0 '<=' t_f( time) '<=' inf }, ...
{ 0 '<=' rocket.velocity '<=' inf }, ...
{ 0 '<=' rocket.height '<=' inf }, ...
{ mf '<=' rocket.mass '<=' m0 }, ...
{ 0 '<=' rocket.fuelMassFlow '<=' Fm } ...
);
% Solving the OCP
sol = ocp.solve('controlIntervals', 60);
%% Plot the results
figure(1)
subplot(311); hold on
sol.plot(time, rocket.velocity)
xlabel('Time')
ylabel('Velocity')
subplot(312); hold on
sol.plot(time, rocket.height)
xlabel('Time')
ylabel('Height')
subplot(313); hold on
sol.plot(time, rocket.mass)
xlabel('Time')
ylabel('Mass')
figure(2); hold on
sol.stairs(time, rocket.fuelMassFlow)
xlabel('Time')
ylabel('F (Control)')
%% Model
function [dx, y] = goddardRocketModel(t, x, u)
% States and control
v = x(1);
h = x(2);
m = x(3);
F = u;
% Parameters
D0 = 0.01227;
beta = 0.145e-3;
c = 2060;
g0 = 9.81;
r0 = 6.371e6;
% Drag and gravity
D = D0*exp(-beta*h);
F_D = sign(v)*D*v^2;
g = g0*(r0/(r0+h))^2;
% Dynamics
dv = (F*c-F_D)/m-g;
dh = v;
dm = -F;
dx = [dv;dh;dm];
% Signals y
y.rocket.velocity = v;
y.rocket.height = h;
y.rocket.mass = m;
y.rocket.fuelMassFlow = F;
y.drag.coefficient = D;
y.drag.force = F_D;
y.gravity = g;
end
Plots